トンネル効果
読み方：トンネルこうか
別名：量子トンネル効果
【英】tunneling, Quantum tunneling
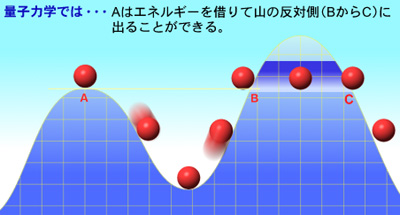
トンネル効果とは、量子力学の分野で、エネルギー的に通常は超えることのできない領域を粒子が一定の確率で通り抜けてしまう現象のことである。
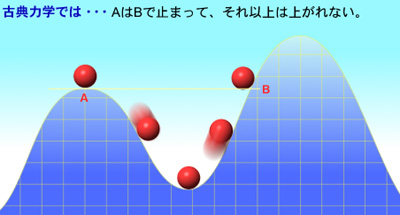
古典的解釈では、物質の運動はポテンシャル障壁と呼ばれる壁に入射すると、衝突して完全に遮られる。しかし原子レベルでは、原子や電子の持つエネルギーが不確定であるため、ポテンシャル障壁よりもエネルギーが大きくなり、結果として障壁を透過してしまうことがある。このような性質がトンネル効果と呼ばれている。例えば原子核のアルファ崩壊もトンネル効果によって説明できる。
トンネル効果は、物理学者の江崎玲於奈によって発見された。この発見によって江崎氏は1973年にノーベル物理学賞を授与されている。
トンネル効果を応用した製品としてはトンネルダイオードを挙げることができる。トンネルダイオードは、ある電圧領域において電圧をかければかけるほど電流が流れにくくなる特性（負性抵抗）を利用して、マイクロ波のような超高周波領域で発振・増幅を行うためのダイオードで活用されている。その他、走査型トンネル顕微鏡などにも応用されている。
参照リンク
トンネル効果 - （九州大学大学院理学研究院）
ツェナーダイオードのトンネル電流 - （図説半導体/電子・デバイス物理）
|
