「離散数学」の解説
数と表現
自然界において、物理的な重さや長さ、時間といった指針による、連続した値は「アナログ」と呼ばれています。これに対して、個数をはじめとした離散的な量による表現は「デジタル」と呼ばれています。
コンピュータは、ある=1、ない=0、といったように、1と0によって値を表現する2進数デジタルの処理を得意としています。2進数で表現される1桁の値は「ビット(bit)」と呼ばれます。ビットは「binary digit」の略です。
数字やアルファベットなどの文字情報を表現するためには、2の8乗=256通りとなる8ビットでひとつの文字を作ります。この8ビットは「バイト(byte)」という単位でまとめて扱われます。
日本語の場合、カナや漢字など多数の文字が用いられるため、1バイトで表現しきることができません。そのため、通常はカナや漢字は2バイトで表現されています。2バイト使用すると2の16乗=65536通りの文字を表現できます。
ビットとバイトは、アルファベット表示だと両方「b」が頭文字となりますが、通例として、ビットを小文字の「b」、バイトを大文字の「B」で書き分け、それぞれ略号としています。
基数変換
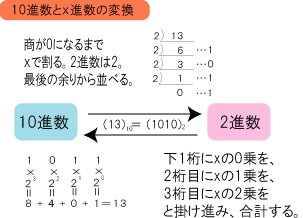
2進法の表現は人間にとっては理解しづらいものです。人間が2進数を扱う場合、一般的には、主に使用している10進法へと変換する方法が用いられます。このような、ある進数から別の進数へと変換する作業は「基数変換」と呼ばれます。
| 2進数 | 10進数 | 8進数 | 16進数 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 |
| 100 | 4 | 4 | 4 |
| 101 | 5 | 5 | 5 |
| 110 | 6 | 6 | 6 |
| 111 | 7 | 7 | 7 |
| 1000 | 8 | 10 | 8 |
| 1001 | 9 | 11 | 9 |
| 1010 | 10 | 12 | A |
| 1011 | 11 | 13 | B |
| 1100 | 12 | 14 | C |
| 1101 | 13 | 15 | D |
| 1110 | 14 | 16 | E |
| 1111 | 15 | 17 | F |
| 10000 | 16 | 20 | 10 |
符号付き2進数
2進数で負の数を扱う場合「符号付き2進数」を用います。符号付き2進数では、最上位のビットが「0」の場合が+で、「1」の場合が−です。
2進数の加算、演算
2進数の加算、演算を行う場合、桁を揃えて下の桁から計算します。
集合
ある条件に基づいてグループ化されたデータの集まりを「集合」と呼びます。「AまたはB」といったように言葉や文章で表現することができます。こうした表現方法は「命題」と呼ばれています。また、命題された集合は「ベン図」により図式化することが可能です。
論理演算
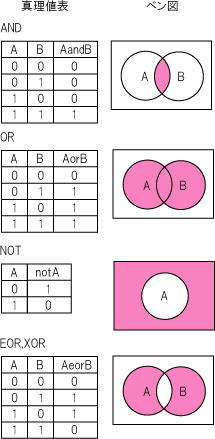
論理演算はベン図と「真理値」で表すと分かりやすくなります。AとBが共に「0(偽)」と「1(真)」の値しかとらないとすれば、その組み合わせは全部で4通りとなります。この組み合わを表にしたものが真理値表と呼ばれるものと、「否定(NOT)」、「論理積(AND)」、「論理和(OR)」、「排他的論理和(EORまたはXOR)」となります。
ポイント
基数の基本的な考え方を理解しましょう。
秀剛の基本的な考え方を理解しましょう。
コンピュータで扱う数値やデータに関する基礎的な理論を知るため、2進数に関する表現と演算、集合と論理演算の基本的な考え方を理解しましょう。